Teste de Sequência Numérica

Apresentar uma sequência numérica e perguntar qual pode ser o próximo número é um dos testes mais comuns na avaliação de inteligência. Este tipo de exercício traduz a capacidade de detectar uma regra não especificada de um conjunto de dados, um recurso que está altamente associado à aprendizagem¹ em si e ao potencial de aprendizagem².

O raciocínio indutivo pode ser útil em muitas situações de resolução de problemas e é comumente usado por matemáticos³.

Instruções

Para cada pergunta, será apresentada uma sequência de números. Você deve selecionar o número que completa a sequência e que deve substituir o ponto de interrogação.

Exemplo: 2 - 4 - 6 - 8 -?

A sequência segue uma estrutura de 2 + 2 + 2 + 2, portanto, o número que completa essa sequência é o 10. Todos os números são múltiplos de 2.

Exemplo de teste:

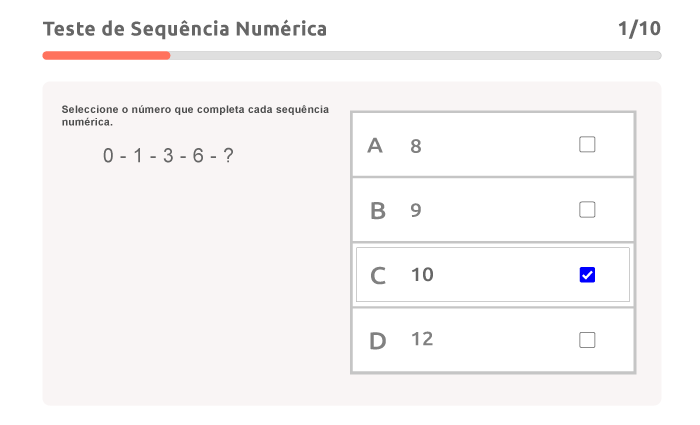
Isenção de Responsabilidade:

Este Teste de Sequência Numérica foi desenvolvido com um propósito educacional e de entretenimento. Os resultados não constituem uma avaliação psicológica ou psiquiátrica de qualquer tipo e podem não oferecer um retrato preciso da aptidão mental do examinado. Não garantimos a exatidão dos resultados e estes não devem ser usados como um indicador das capacidades do indivíduo para um fim específico.

As respostas podem ser registradas e usadas para fins de investigação ou para serem distribuídas de outra forma. Todas as respostas são registradas anonimamente.

Série numérica - padrões comuns

Série monótona

As séries monótonas são criadas apenas por adição e subtração, portanto seus padrões estão entre os mais fáceis de identificar em qualquer teste de raciocínio numérico.

No entanto, existem variações nas séries básicas que podem dificultar a identificação da regra que as rege. Essas variações geralmente dependem de padrões não percebidos imediatamente à primeira vista.

Um exemplo de uma série monótona simples pode ser 1 - 2 - 3 - 4. Aqui o padrão seria adicionar +1 a cada número para formar a sequência.

No caso de uma série mais complexa, poderia acontecer que o terceiro número seja obtido somando a diferença entre o primeiro e o segundo e adicionando essa diferença ao padrão base.

Por exemplo: 0 - 2 - 6 - 12 - 20

Nesta sequência, o padrão base é adicionar +2 entre os números. No entanto, a esse padrão também se soma a diferença entre cada um dos dígitos:

0 - 2 (+2 +2) 6 (+2 +4) 12 (+2 +6) 20

Série exponencial

As séries exponenciais podem ser obtidas por meio de multiplicação e divisão, embora também possam incluir adições e subtrações para criar séries e padrões mais complexos.

Nas séries simples, os números são sempre multiplicados ou divididos pelo mesmo dígito. Tomemos a série 2 - 4 - 16 - 128 como exemplo. O salto de 4 para 16 e depois para 128 já sugere que esta provavelmente não é uma série monótona. Um olhar mais atento pode dizer que cada número é multiplicado por si mesmo para encontrar o seguinte.

2 x 2 = 4
4 x 4 = 16
16 x 16 = 128

Nas mais complexas, o número responsável pela multiplicação pode mudar seguindo um padrão de adição ou subtração.

Por exemplo, você pode ter a sequência 2 - 4 - 12 - 48. Nesse caso, a série exponencial está sendo afetada pela adição de +1 ao número pelo qual os dígitos estão sendo multiplicados:

2 x 2 = 4
3 x 4 = 16
4 x 16 = 48

Assim, o próximo número nesta série seria 240 (5 x 48).

Uma boa dica para lembrar no caso de séries exponenciais é tentar dividir cada número pelo anterior para verificar se são múltiplos e se existe um padrão aí.

Padrão alternado

Nesse tipo de série, o padrão não é imediatamente óbvio. Normalmente, os números podem aumentar ou diminuir nas sequências, com saltos que não parecem lógicos à primeira vista.

Como o nome sugere, esses tipos de séries ocultam um padrão alternado que pode conter adições, subtrações, multiplicações e divisões, isoladas ou combinadas. Um exemplo de um padrão alternado simples seria 1 - 3 - 6 - 8 - 11. O padrão aqui é alternar entre adicionar +2 e +3 ao número anterior:

1 + 2 = 3
3 + 3 = 6
6 + 2 = 8
8 + 3 = 11

Os padrões mais complexos podem ser mais longos. Uma boa dica é sempre verificar se existe uma multiplicação ou adição quando o número aumenta ou uma subtração ou divisão quando diminui.

Padrões entrelaçados

As sequências entrelaçadas contêm dois ou mais padrões independentes um do outro. Nesse tipo de série, não há relação entre os números que se seguem diretamente.

Em sequências entrelaçadas simples, os padrões tendem a saltar entre as posições pares e ímpares. Tomemos a seguinte sequência como exemplo: 2 - 0 - 4 - 4 - 6 - 8. Aqui as posições ímpares aumentam em +2 enquanto as posições pares aumentam em +4.

Quanto mais longas as sequências, mais padrões elas contêm e quanto mais longos os saltos entre os padrões, mais difícil é detectar as regras que as governam.

Frações

Existem dois tipos de séries numéricas contendo apenas frações. O mais comum em testes de QI tende a seguir uma das lógicas mencionadas acima. Ou seja, seguem os mesmos padrões dos números inteiros, mas são apresentados na forma de frações.

O segundo tipo é mais complicado, porque pode conter qualquer um dos padrões antes mencionados, por vezes misturados, no numerador e denominador ao mesmo tempo.

Referências:

¹ Angluin D., Smith C.H. (1983). Inductive inference: Theory and methods. Comput. Surveys, 15 (1983), pp. 237-269.

² Csapó, B. (1997). The Development of Inductive Reasoning: Crosssectional Assessments in an Educational Context. International journal of behavioral development. 20 (4), 609–626.

³ Pólya, G. (1954). Induction and Analogy in Mathematics. Princeton University Press. p. 120.